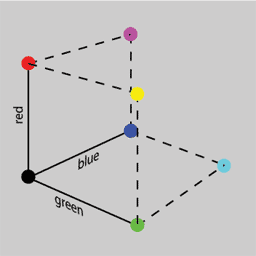
Now imagine putting the black corners of the three pictures we have shown so far next to each other and folding the three squares together to make a corner of a cube.
The right hand picture here then shows how we can consider the red, green and blue edges to be coordinate axes for the colour space. Any point inside the cube that we have started to construct has a certain amount of each of the three additive primary colours, red, green and blue. By imagining points inside the cube we can see that we can represent far more colours than those which lie merely on the three faces of the cube that we have looked at so far.
There is an important colour missing from the story. Where is white?